Data-Parallel C++ with oneAPI/SYCL#
A growing challenge for the HPC community has been performance portability , i.e., the ability to maintain consistent application performance in the context of increasing complexity and heterogeneity of hardware, as well as the additional need to maintain developer productivity and computational precision. The intersection of performance, portability, and productivity goals (P3) has also been the focus of an annual workshop at the Supercomputing Conference (SC) for several years.
One of the key frameworks to emerge in response to the P3 challenge is oneAPI, which promises to be a single application programming interface (API) that can be used to program all available architectures. Programming is done using a modern dialect of C/C++, known as Data-Parallel C++ and SYCL, a standard for higher-level abstractions for parallelism and concurrency. While oneAPI is not the only alternative, the ability to write largely device-independent programs is a promising direction with great potential to exploit parallelism as the world moves toward more “on chip” heterogeneity and clusters thereof.
Running Example: Trapezoidal Integration#
Sometimes, a program needs to integrate a function (i.e., calculate the area under a curve). We might be able to use a formula for the integral, but this isn’t always possible. An easy alternative approach, suitable for numeric integration, is to approximate the curve with straight line segments and calculate an estimate of the area from them.
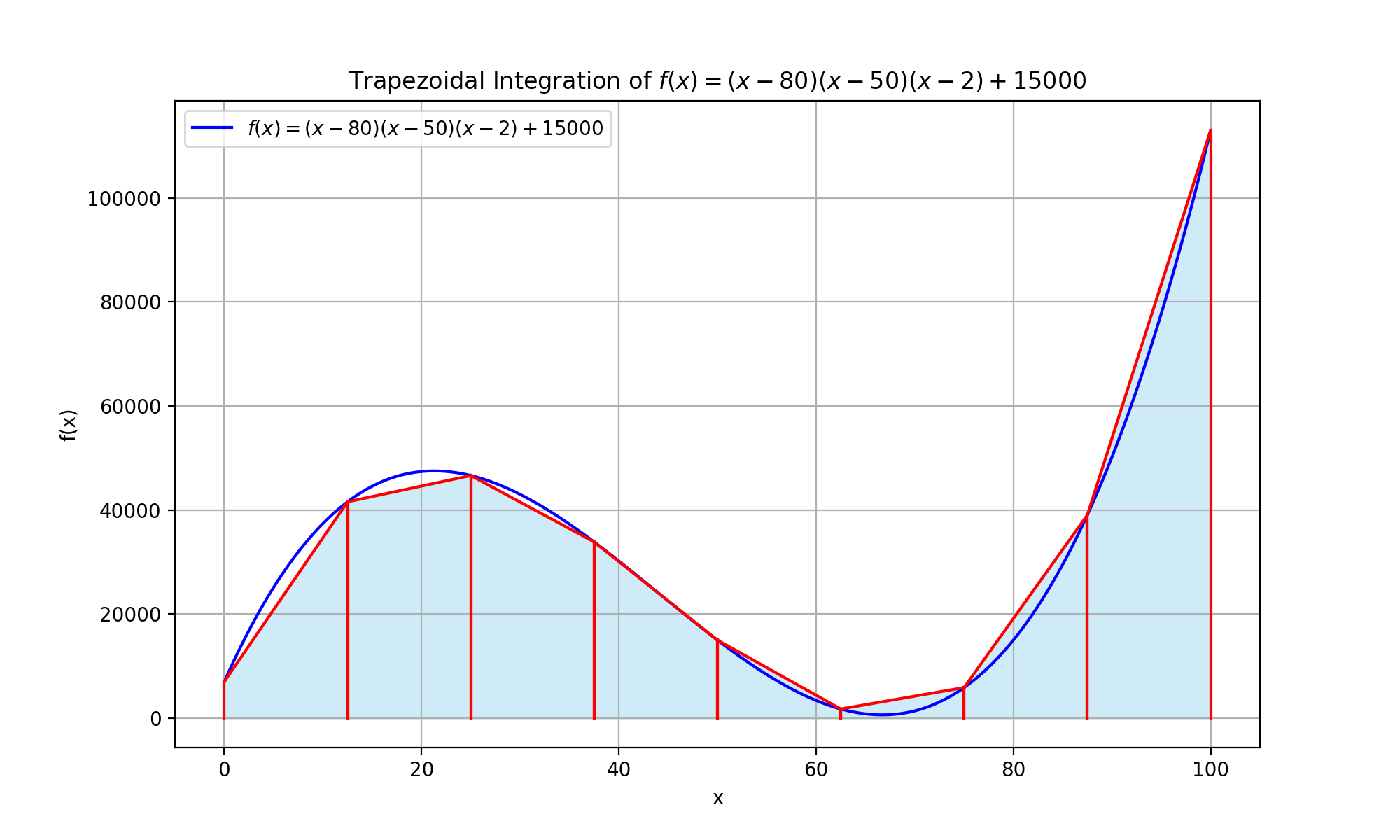
Concretely, to find the area under the curve from a to b, we approximate the function by dividing the domain from a to b into g equally sized segments. Each segment is (b – a) / g long. Let the boundaries of these segments be x0 = a, x1, x2, … , xg = b. The polyline approximating the curve will have coordinates (x0, f(x0)), (x1, f(x1)), (x2, f(x2)), …, (xg, f(xg)). This allows us to approximate the area under the curve as the sum of g trapezoids.
For the interested reader, you can see the code to produce this figure using Python’s remarkable matplotlib package! See also Trapezoidal Plot on Google Colab.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
import re
# Define the symbolic function
x = sp.Symbol('x')
f_sym = (x - 2) * (x - 50) * (x - 80) + 15000
f_lambda = sp.lambdify(x, f_sym, 'numpy')
# Convert the symbolic expression to a sanitized string for filename
filename_data = re.sub(r'[\*\^\(\)/\+\-\s]', '_', str(f_sym)) + "_trapezoids.csv"
filename_base_plot = re.sub(r'[\*\^\(\)/\+\-\s]', '_', str(f_sym)) + "_trapezoidal_integration"
# Define the range
a, b = 0, 100
n = 8 # number of trapezoids
h = (b - a) / n
x_intervals = np.linspace(a, b, n+1)
# Populate DataFrame for Trapezoids
data = {
'x_left': x_intervals[:-1],
'x_right': x_intervals[1:],
}
data['y_left'] = f_lambda(data['x_left'])
data['y_right'] = f_lambda(data['x_right'])
data['area'] = 0.5 * h * (data['y_left'] + data['y_right'])
df = pd.DataFrame(data)
# Save DataFrame to CSV
df.to_csv(filename_data, index=False)
# Plotting
plt.figure(figsize=(10,6))
x_vals = np.linspace(a, b, 1000)
plt.plot(x_vals, f_lambda(x_vals), 'b-', label=f'$f(x) = {sp.latex(f_sym)}$')
for index, row in df.iterrows():
x0, x1 = row['x_left'], row['x_right']
y = [row['y_left'], row['y_right']]
plt.fill_between([x0, x1], y, color='skyblue', alpha=0.4)
plt.plot([x0, x1], y, 'r-')
plt.plot([x0, x0], [0, row['y_left']], 'r-')
plt.plot([x1, x1], [0, row['y_right']], 'r-')
plt.title(f'Trapezoidal Integration of $f(x) = {sp.latex(f_sym)}$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
# Save to both PDF and PNG
plt.savefig(filename_base_plot + ".pdf")
plt.savefig(filename_base_plot + ".png")
# Show the plot
#plt.show()
print(f"Data saved to {filename_data}")
print(f"Plots saved to {filename_base_plot}.pdf and {filename_base_plot}.png")
Data-Parallel C++ Implementation#
Our trapezoidal integration exemplar example demonstrates various key aspects of data-parallel C++ programming using Intel’s oneAPI platform, which is based on the SYCL cross-platform standard for heterogeneous accelerator-based computing. Although the example is embarrassingly parallel, it nevertheless exhibits various non-trivial challenges that we will discuss in detail.
The exemplar’s sequential version illustrates the underlying fused-loop map-reduce algorithm, which maps each adjacent pair of function values to a trapezoid area and, in the same loop body, reduces (adds) the area to the cumulative result.
if (run_sequentially) {
device_name = "sequential";
std::vector values(size, 0.0);
auto result{0.0};
mark_time(timestamps,"Memory allocation");
spdlog::info("starting sequential integration");
// populate vector with function values and add trapezoid area to result
// the inner loop performs a finer-grained calculation
values[0] += f(x_min);
for (auto i{0UL}; i < number_of_trapezoids; i++) {
const auto x_pos{x_min + i * dx};
result += outer_trapezoid(grain_size, x_pos, dx_inner, half_dx_inner);
values[i + 1] = f(x_pos);
}
mark_time(timestamps, "Integration");
spdlog::info("result should be available now");
fmt::print("result = {}\n", result);
if (show_function_values) {
spdlog::info("showing function values");
print_function_values(values, x_min, dx, x_precision, y_precision);
mark_time(timestamps, "Output");
}
}
We’ll see shortly how to write the data-parallel version of this algorithm in DPC++.
The Platform: Intel oneAPI/Khronos SYCL#
The SYCL standard defines high-level abstractions for parallel computing using modern C++, in an effort by Khronos to influence the ISO C standard to support heterogeneous computing. Data-Parallel C++ (DPC++), a part of Intel’s oneAPI standard, is an implementation of SYCL. Intel provides remote access to various types of accelerator hardware, including GPUs and FPGAs, through its DevCloud program.
Device Selection and Task Queues#
A typical DPC++ program starts with the selection of one or more accelerator devices based on criteria of varying specificity. In our exemplar, the user can choose between running the code on the host CPU and an available accelerator:
sycl::device device { run_cpuonly ? sycl::cpu_selector_v : sycl::default_selector_v };
The interface between the programmer and the chosen device is a queue, to which we can later submit commands for execution on the device.
sycl::queue q{device, dpc_common::exception_handler};
mark_time(timestamps,"Queue creation");
device_name = q.get_device().get_info<sycl::info::device::name>();
spdlog::info("Device: {}", device_name);
If we do not explicitly specify a device when creating our queue, the queue will automatically select the most suitable available device on the current hardware. Also, we can choose between a simple in-order queue or, as we have done here, we can have the queue figure out the best order for executing the submitted commands without deadlocking.
In addition to programmatic device selection through the API, setting the ONEAPI_DEVICE_SELECTOR environment variable may be required to help oneAPI find specific accelerators;
the section Running on hardware with NVIDIA GPUs shows an example of this mechanism.
parallel_for() Construct#
At the heart of SYCL’s support for data parallelism lies the parallel_for() construct, which allows us to express the instructions that should execute in parallel.
While also providing varying degrees of control over splitting up the workload and assigning it to the accelerator device, SYCL is able to come up with a suitable assignment that maximizes parallelism based on the capabilities of the device.
q.submit([&](auto & h) {
const sycl::accessor t{t_buf, h};
h.parallel_for(size, [=](const auto & index) {
t[index] = outer_trapezoid(grain_size, x_min + index * dx, dx_inner, half_dx_inner);
});
}); // end of command group
In this example, f() represents the computation we perform in parallel on each data item.
As shown below, separating f into its own compilation unit enables us to unit-test it, as well as choose a specific implementation of f at build time.
To combine the trapezoids’ areas into a single result, while allowing SYCL to maximize parallelism, we can use parallel_for() along with a suitable reduction operation, i.e., sycl::plus<>().
q.submit([&](auto & h) {
const sycl::accessor t{t_buf, h};
const auto sum_reduction{sycl::reduction(r_buf, h, sycl::plus<>())};
h.parallel_for(sycl::range<1>{number_of_trapezoids}, sum_reduction, [=](const auto & index, auto & sum) {
sum.combine(t[index]);
});
}); // end of command group
Separate Compilation and External Functions#
Separate compilation of source files helps us decompose a software system into smaller modules. This has multiple benefits, including separation of concerns, unit testing, easier collaborative development, and the ability to defer certain decisions (e.g., what function we’re integrating) until build time.
In our exemplar, we’ll want to unit-test the integrand f and defer choosing a specific implementation of that function until build time.
To be able to separately compile the function and call it inside a DPC++ kernel, we declare it in this SYCL-specific way:
#include <sycl/sycl.hpp>
SYCL_EXTERNAL double f(double x);
The following cube function is the specific integrand we use in our performance experiments:
double f(const double x) {
return 3 * pow(x, 2);
}
In addition, for testability, we have modularized the functions for computing a single trapezoid and an outer trapezoid (corresponding to the parallel grain size).
Conceptually, the outer_trapezoid function is parametric in the integrand f.
Because SYCL does not support passing a function pointer to a kernel task, however, this parametricity is implicit based on the build-time choice of a specific implementation of f.
The corresponding header file looks like this, with f not appearing as a formal argument to outer_trapezoid.
#ifndef INTEGRATION_H_
#define INTEGRATION_H_
#include <sycl/sycl.hpp>
// {{UnoAPI:trapezoid-interface:begin}}
SYCL_EXTERNAL double single_trapezoid(double f1, double f2, double dx);
// {{UnoAPI:trapezoid-interface:end}}
SYCL_EXTERNAL double outer_trapezoid(
const int grain_size,
const double x_pos,
const double dx_inner,
const double half_dx_inner
);
#endif // INTEGRATION_H_
We show the implementation of these functions in the chapter on performance below; it is also available here.
Another Example: Calulating Pi using the Monte Carlo Method#
This example follows a similar pattern as the trapezoidal integration one. Conceptually, each player throws a given number of darts, where those that fall within the quarter circle are counted toward the calculation of \(\pi\). The various players operates in parallel with and independently of all other players To improve randomization, each player’s random number generator instance starts with a differen seed offset.
q.submit([&](auto &h) {
const auto c = c_buf.get_access<sycl::access_mode::write>(h);
h.parallel_for(number_of_players, [=](const auto index) {
const auto offset = 37 * index.get_linear_id() + 13;
oneapi::dpl::minstd_rand minstd(seed, offset);
oneapi::dpl::ranlux48 ranlux(seed, offset);
//constexpr double R{1.0};
//oneapi::dpl::uniform_real_distribution<double> distr(0.0, R);
constexpr uint64_t R{3037000493UL}; // largest prime <= sqrt(ULONG_MAX / 2)
oneapi::dpl::uniform_int_distribution<uint64_t> distr(0, R);
const auto r_square{R * R};
auto darts_within_circle{0UL};
for (auto i{0UL}; i < number_of_darts; i++) {
const auto x{use_ranlux ? distr(ranlux) : distr(minstd)};
const auto y{use_ranlux ? distr(ranlux) : distr(minstd)};
const auto d_square{x * x + y * y};
if (d_square <= r_square)
darts_within_circle++;
}
c[index] = darts_within_circle;
});
});
After all the players are done, we perform a reduction to combine the number of darts within the quarter circle.
q.submit([&](auto &h) {
const auto c{c_buf.get_access<sycl::access_mode::read>(h)};
const auto sum_reduction{sycl::reduction(s_buf, h, sycl::plus<>())};
h.parallel_for(sycl::range<1>{number_of_players}, sum_reduction, [=](const auto index, auto &sum) {
sum.combine(c[index]);
});
});
A sample run looks like this:
[2023-10-09 20:12:49.704] [info] 4 players are going to throw 1000000 darts each
[2023-10-09 20:12:49.704] [info] using minstd engine with real distribution
[2023-10-09 20:12:49.704] [info] randomization is off
[2023-10-09 20:12:49.763] [info] Device: Intel(R) Core(TM) i5-1030NG7 CPU @ 1.10GHz
[2023-10-09 20:12:49.763] [info] Max workgroup size: 8192
[2023-10-09 20:12:50.474] [info] done submitting to queue...waiting for results
[2023-10-09 20:12:50.474] [info] result[0] = 786512
[2023-10-09 20:12:50.474] [info] result[1] = 786064
[2023-10-09 20:12:50.474] [info] result[2] = 786509
[2023-10-09 20:12:50.474] [info] result[3] = 786054
[2023-10-09 20:12:50.474] [info] sum = 3145139
pi = 3.145139